Defining mixing matrices for generation of non-random sequence pools

Mixing Matrix

Definition

The Mixing matrix M, for pool synthesis using four vials or ports, is a 4x4 matrix that specifies the molar fractions of nucleotide components A, C, G and U in the four vials.

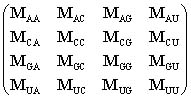Thus, the (ij)-element of M (i.e.,M_ij) denotes the molar fraction of base j in vial "for base i". For example, M_AU is the fraction of U nucleotides in vial for A, M_AA is the fraction of A in vial A, and M_UA is the fraction of A in vial U. Thus, the elements of each row of the matrix sum to unity: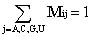

Examples

- Random matrix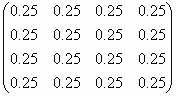

- Fixed matrix

- Symmetric matrix with 0.15 mutation rate = MM1

- Asymmetric matrix = MM15

Biological Motivations

Mixing matrices with symmetric elements, M_AU = M_UA, M_CG = M_GC, M_GU = M_UG, are considered to preserve base pairs. Such matrices cover the sequence subspace approximating covariance mutations (e.g. AU to UA, CG to GC, GU to UG). Alternatively, to disrupt stems and generate new structures, we can consider mixing matrices that do not preserve base pairs. Such matrices include asymmetric matrices without the property of covariance mutations. Non-covariance mutations, including random mutations, are commonly used to generage sequence pools for in vitro selection applications.

Five Classes of Mixing Matrices

The mixing matrix classes motivated by biological mutations are characterized by the following matrix elements: (A) varying diagonal elements M_ii with the condition M_AA = M_CC = M_GG = M_UU, (B) M_CC = M_GG = 1, (c) M_AA = M_UU = 1, (D) M_AC = M_UG = 1, and (E) M_CA = M_GU = 1. Within each class, several mixing matrices are constructed whose elements are distributed uniformly in steps of 0.25. A total of 22 mixing matrices representing the five classes are displayed as follows:

The matrix classes to which they belong are as follows: (A) matrices 1-6, (B) matrices 7-10, (C) matrices 11-14, (D) matrices 15-18, and (E) matrices 19-22. Note that in vitro experiments effectively use random pools generated by a constant 4x4 mixing matrix where all 16 elements are 0.25; this corresponds to our matrix 4.

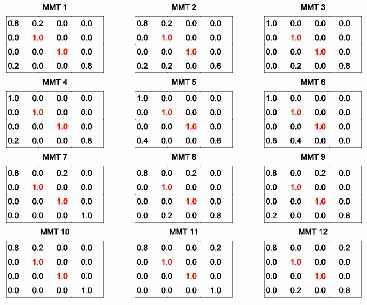To increase the population of complex folds like the tRNA-like 5₃ tree motif, we consider refining the mixing matrices 7-9. Remarkably, 12 of 3136 mixing matrices for tRNA-like topology fulfill our requirement forming 5₃ motifs. We use these “MMT” matrices to generate graph-structural distributions with tRNA shapes.
For example, MMT6 generates 51% of tRNA-like 5₃ tree motif with 15 mutations out of 81 bases.

Coverage of Sequence Space Regions Generated by Mixing Matrix Classes

The global 2D and 3D clustering of sequences generated by 22 mixing matrices using starting sequences for the modified p5abc and 70S RNAs show that the sequences generated by the five mixing matrix classes cover distinct regions of the sequence space. We use Hamming distances together with a clustering technique - multidimensional scaling (MDS) method implemented in R statistical package - to map the RNA sequence/structure space.

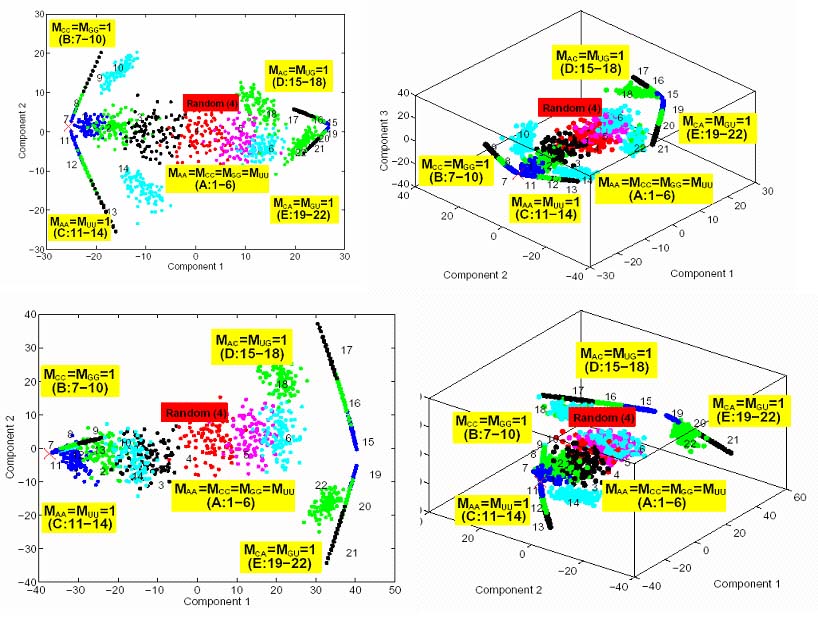In the figure, axes represent two or three largest components of the projection. Each color represents a sequence pool generated by one of the 22 mixing matrices; the X mark on the left represents result for an invariant sequence transformation corresponding to diagonal matrix M_ii = 1. The mixing matrices are grouped into five classes (A-E) according to their matrix class A. Intriguingly, the random mixing matrix 4 (MM4) produces sequences that are localized in sequence space, showing that the standard approach does not provide an efficient sampling of diverse regions of sequence space in agreement with observations.