



|




|
|
Our pool design algorithm is based on analyses of sequence and structure spaces to allow design of specific structures,
including novel RNA-like motifs identified using
graph theory analysis.
The algorithm below assumes we have available reference data
that relate mixing matrices
and starting sequences to
motif distributions in resulting pools. By knowing the structural
distributions of various sequence space regions, we optimize the choice of starting sequences, mixing matrices, and
associated weights to approximate the target structured pool.
| ||||||||||
|
Our pool design algorithm involves the following steps: (i) Specify a target distribution (T) of topologies/shapes. (ii) Define candidates for starting sequences and mixing matrices that aim to cover the sequence space. In this web server, we use mainly 6 starting sequences and constructed 22 mixing matrices to cover the sequence space. (iii) Compute motif distributions corresponding to all starting sequence / mixing matrix pairs. This step analyzes pool structural diversity. (iv) Choose the number of mixing matrices to approximate the designed pool.
(v) Find an optimal combination of starting sequences (Si) and mixing matrices (Mi) and
associated weights (
| ||||||||||
|
Optimization Procedures for Step (v)We approximate a target structural distribution by optimizing a set of starting sequence/mixing matrix pairs based on pool structural frequency data. Generally, we consider a designed pool composed of k subpools, each generated with a mixing matrix/starting pair and associated with a weight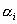 : : 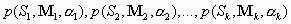 ,
where ,
where 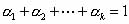 and and 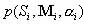 denotes synthesizing denotes synthesizing 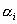 fraction of
the pool sequences using starting sequence Si and mixing matrix Mi.
Optimization of the three pool parameters Si, Mi and fraction of
the pool sequences using starting sequence Si and mixing matrix Mi.
Optimization of the three pool parameters Si, Mi and 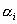 can be formulated as follows: If the nx1 matrix
can be formulated as follows: If the nx1 matrix 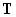 is the target distribution with
Ti fractions of structures 1, 2,…, n and is the target distribution with
Ti fractions of structures 1, 2,…, n and 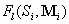 is the pool fraction of structure
l generated by starting sequence Si and
mixing matrix Mi, the pool parameters
( is the pool fraction of structure
l generated by starting sequence Si and
mixing matrix Mi, the pool parameters
(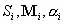 ) can be optimized by the following equation: ) can be optimized by the following equation:
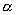 = =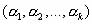 subject to the conditions subject to the conditions
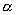 1
+ 1
+ 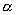 2 + ... + 2 + ... + 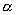 k = 1 and k = 1 and
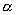 i i 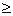 0.
Since experimental implementation of pool synthesis is simpler with fewer mixing matrices, we will consider below the
solution of 0.
Since experimental implementation of pool synthesis is simpler with fewer mixing matrices, we will consider below the
solution of 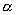 for k=2;
the optimization procedure can be generalized. Formula (1) with only two mixing matrices M1 and
M2 reduces to: for k=2;
the optimization procedure can be generalized. Formula (1) with only two mixing matrices M1 and
M2 reduces to:
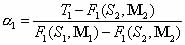 The estimated pool fractions for the other shapes or topologies 2,3,…,n are derived from the known 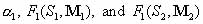 as follows: as follows:
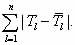 . The above procedure will allow us to obtain the optimized parameters . The above procedure will allow us to obtain the optimized parameters
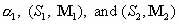 for a target distribution for a target distribution 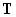 . The convergence of the procedure depends
on the number of mixing matrices and starting sequences, or coverage of the sequence/structure space. . The convergence of the procedure depends
on the number of mixing matrices and starting sequences, or coverage of the sequence/structure space.
| ||||||||||
